What is FreeLM?

FreeLM is a language-modeling toolkit that builds N-gram models from training text. It is released under the Apache license v2.0. It generates language models in the standard ARPA format. These can be used, for instance, in speech recognition and machine translation.

FreeLM is not intended primarily for language modeling research. It is intended to be efficient and very scalable, but it is not designed with flexibility in mind. In fact, FreeLM does not support many standard methods such as absolute discounting, Kneser-Ney, etc. It only really supports one recipe, and it is not a standard, previously published one. However, it is better than the standard (Kneser-Ney) approach. Our approach is better partly because it gives slightly better perplexity for a standard LM-building task, but mainly because it allows us to handle things like entropy pruning (like ``Stolcke pruning''), interpolation, low-count removal, etc., in a consistent way.

The main idea

This section requires a basic background in language modeling; we recommend ``A Bit of Progress in Language Modeling'' by Joshua Goodman. If you're not a language modeling person, you don't need to understand this section: just know that we are saying this toolkit will give better results than whatever you're already using.

The main idea of the toolkit is to preserve sums of counts, or put another way, to always deal with ``real'' counts. Suppose we did traditional Kneser-Ney smoothing with D=1, i.e. we discount one count. This has the property that the count we add to the backoff state (i.e. the backoff count) is the same as what we discounted (i.e. 1). This property is lost in Kneser-Ney with D not equal 1, and it is lost in a more profound way with ``modified Kneser Ney'', where we discount different amounts depending what the original count was. Also consider that the original justification of Kneser-Ney pruning relied on a property very like the one we are talking about-- it relates to ``preserving marginals'' over events like seeing a particular word.

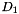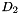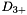The original idea behind this toolkit was that we would do modified interpolated Kneser-Ney smoothing, which is generally considered the state of the art (among practical, fast techniques), but modify it so that instead of using the count-of-counts in the backoff states, we use the actual amount discounted, i.e. the quantities $D_1$ , $D_2$ , and $D_{3+}$ . Of course, once we go to partial counts the normal formulas for determining what these quantities should be, no longer apply. Firstly, we point out that this is no great loss since these formulas are not valid anyway in interpolated Kneser-Ney. We intended to just search over these quantities. 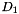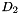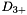But then notice that since the counts are no longer integers, having three separate backoff constants $D_1$ , $D_2$ , and $D_{3+}$ is no longer applicable. We need a continuously varying backoff amount. We experimented with a few formulas for this, but in the end it seems like a formula of the following is close to ideal, and giving it extra parameters doesn't give any improvement for the data we tested: 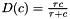$D(c) = \frac{ \tau c } { \tau + c}$ , where $$ is a discounting constant for the N-gram order concerned. This function gradually approaches 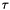$\tau$ as the count gets large. We optimize the 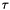$\tau$ values for each order by minimizing the perplexity of held-out data.

There is a slight complication which we won't get to in this interview, which relates to how we deal with discarding small counts (this is a standard method used to get rid of small counts). In order to do this consistently, we do this by applying standard absolute discounting, before the 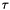$\tau$ discounting we describe above. If absolute discounting has already been applied, we modify the formula for the 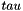$tau$ discounting in order to approximate as closely as possible what would have happened if we had never done absolute discounting but had done 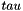$tau$ discounting from the start.

Efficient implementation

The second unique feature of this toolkit is its efficient and scalable implementation. It is based on the idea described in the technical report "MSRLM: a scalable language modeling toolkit" by Patrick Nguyen et al, Microsoft Research, November 2007. They use the term ``backsorted trie''. What this means is we sort the n-gram counts initially on their history, but in reverse order. So a count like "TO THE SHOP" becomes "TO THE -> SHOP" which we reverse to "THE TO -> SHOP" and we sort on this. We write N-gram counts to disk in a format where a line might look like

THE TO  SHOP  4.0

Multiple spaces above are supposed to represent the tab character. The tab is important because we have N-grams of all orders in the same file, and the tab ensures they end up in the order we want them to be in. This sorting has a special benefit for doing N-gram discounting and certain other N-gram operations, because it means we can process the file of sorted N-grams sequentially, but always only keep a small subset of them in memory; and yet we always have in memory what we need to do the operation we're doing. Basically, we always keep in memory only a single N-gram history state of any given order, and whenever we have a particular history state in memory, we have the backoff states of all orders corresponding to that state (so for instance, we always have the unigram backoff state in memory). Programs may write out their N-gram counts out of order, and we use the UNIX program ``sort'' to do the heavy lifting of putting them back in order.

In fact we never deal with actual words like "THE" in our N-gram counts file. Instead, we first map all words to a short quasi-textual representation, so that "THE", since it is very common, would get mapped to a short word like "D". (The first three words "A", "B" and "C" are reserved for the beginning-of-sentence symbol <s>, the end of-sentence symbol </s> and the unknown-word symbol <UNK>). Aside from the efficiency advantages of this, we can ensure that we never have to deal with words with punctuation symbols in them.

Status of the project

This project is actively under development. It should be stabilized in a month or two.